Sort the matrix diagonally

Let's try to solve one of the LeetCode challenges in easy and hard mode at the same time.

• Link to the problem: https://leetcode.com/problems/sort-the-matrix-diagonally/

Problem description

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

Example

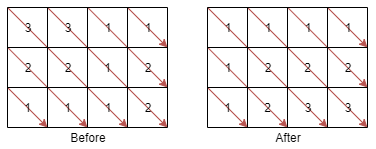
Skeleton and initial adjustments

We are given the following skeleton for the C++ and the given challenge:

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {

    }
};

The task is to sort the passed matrix diagonally and then return it. First of all, I don't like to solve this in a web browser, so we'll need to adjust it accordingly for running it locally. We'll start by including the vector header and using fully-qualified namespaces¹ and also adding few tests:

#include <cassert>
#include <vector>

using matrix = std::vector<std::vector<int>>;

class Solution {
public:
    matrix diagonalSort(matrix& mat)
    {
    }
};

static void test_case_1()
{
    // Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
    // Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

    Solution s;
    assert((s.diagonalSort(std::vector { std::vector { 3, 3, 1, 1 },
                std::vector { 2, 2, 1, 2 },
                std::vector { 1, 1, 1, 2 } })
        == std::vector { std::vector { 1, 1, 1, 1 },
            std::vector { 1, 2, 2, 2 },
            std::vector { 1, 2, 3, 3 } }));
}

static void test_case_2()
{
    // Input: mat =
    // [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
    // Output:
    // [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

    Solution s;
    assert((s.diagonalSort(std::vector { std::vector { 11, 25, 66, 1, 69, 7 },
                std::vector { 23, 55, 17, 45, 15, 52 },
                std::vector { 75, 31, 36, 44, 58, 8 },
                std::vector { 22, 27, 33, 25, 68, 4 },
                std::vector { 84, 28, 14, 11, 5, 50 } })
        == std::vector { std::vector { 5, 17, 4, 1, 52, 7 },
            std::vector { 11, 11, 25, 45, 8, 69 },
            std::vector { 14, 23, 25, 44, 58, 15 },
            std::vector { 22, 27, 31, 36, 50, 66 },
            std::vector { 84, 28, 75, 33, 55, 68 } }));
}

int main()
{
    test_case_1();
    test_case_2();

    return 0;
}

We need to return the matrix, but we're given a reference to the input matrix. We can easily abuse the C++ here and just switch the reference to value, this way the matrix will be copied when passed to the function, we can sort the copy and just return it back. And we also get yelled by the compiler for the fact that the method doesn't return anything yet, so to make it “shut up” we will just return the input for now:

-    matrix diagonalSort(matrix& mat)
+    matrix diagonalSort(matrix mat)
     {
+        return mat;
     }

Now, we get the copy and we're good to go.

Naïve solution

As you may know, C++ offers a plethora of functions that can be used to your advantage, given that you know how to “bend” the data structures accordingly.

What does that mean for us? Well, we have an std::sort, we can use it, right? Let's have a look at it:

template< class RandomIt >
void sort( RandomIt first, RandomIt last );

This overload is more than we need. What does it do? It just sorts the elements in the range [first, last) using operator< on them. We can't sort the whole matrix using this, but… we can sort just »one« diagonal without doing much work on our end.

What is the RandomIt type though? If we look more into the documentation, we can easily find the requirements for it and also learn that it's a random access iterator and allows swapping its values at the same time.

Random access iterator

What is the random access iterator though? We can find it in a documentation and see the following description:

A LegacyRandomAccessIterator is a LegacyBidirectionalIterator that can be moved to point to any element in constant time.

After that we can see all the requirements for it being listed. I don't feel like reading them right now, so we will just use it and see where the compilation blows up, i.e. “compiler-assisted development”² if you will ;)

Now we know that we can use std::sort to sort the diagonal itself, but we also need to get the diagonals somehow. I'm rather lazy, so I'll just delegate it to someone else³. And that way we get

matrix diagonalSort(matrix mat)
{
    // we iterate over the diagonals
    for (auto d : diagonals(mat)) {
        // and we sort each diagonal
        std::sort(d.begin(), d.end());
    }

    // we take the matrix by copy, so we can sort in-situ and return the copy
    // that we sorted
    return mat;
}

This solution looks very simple, doesn't it? Well, cause it is. Let's try compiling it:

matrix-sort.cpp:11:23: error: use of undeclared identifier 'diagonals' [clang-diagnostic-error]
        for (auto d : diagonals(mat)) {
                      ^
Found compiler error(s).
make: *** [makefile:14: tidy] Error 1

OK, seems about right. We haven't implemented the diagonals yet. And based on what we've written so far, we need a function or a class diagonals that will give us the diagonals we need.

Implementing the diagonals

Cool, so we need the function that will let us go through each and every diagonal in our matrix. We use the for-range loop, so whatever we get back from the diagonals must support .begin() and .end(). Since I am a masochist, we will do such functionality for a matrix of any type, not just the int from the challenge.

As I said, we need to be able to

• construct the object
• get the beginning
• get the end (the “sentinel”)

template <typename T>
class diagonals {
    using matrix_t = std::vector<std::vector<T>>;

    matrix_t& _matrix;

public:
    diagonals(matrix_t& m)
        : _matrix(m)
    {
    }
    diagonals_iter begin()
    {
        /* TODO */
    }
    diagonals_iter end()
    {
        /* TODO */
    }
};

Now we have a diagonals that we can use to go through the diagonals. We haven't implemented the core of it yet. Let's go through what we have for now.

We have a templated class with templated T that is used as a placeholder for any type we would store in the matrix. Because I'm lazy, I have defined the matrix_t type that is a “shortcut” for std::vector<std::vector<T>>, so I don't have to type it out all the time. Of course, we need to store the matrix, we are given, as a private attribute. And then just have the constructor and the 2 methods we need for the for-range.

Iterating over diagonals

Now that we have an object that will allow us to iterate through the diagonals, we need to implement the iterating itself. We need to go through all of them, so we have multiple options how to do so. I have decided to start from the “main” diagonal that starts at (0, 0) index and then proceed with the diagonals starting in the first row, followed by the rest of the diagonals in the first column.

We need to be able to tell that we've iterated through all of them, and also we need to know which diagonal is next. For that purpose we will pass the indices of the first cell on the diagonal. That way we can always tell how to move forward.

We will start by updating the begin and end to reflect our choice accordingly.

diagonals_iter begin() { return diagonals_iter { _matrix, 0, 0 }; }
diagonals_iter end() { return diagonals_iter { _matrix, 0, _matrix.size() }; }

For the begin we return the first diagonal that starts at (0, 0). And because we have decided to do the diagonals in the first column at the end, the first diagonal that is not a valid one is the one at (0, height). Apart from the indices, we also need to pass reference to the matrix itself.

note

You may have noticed that we also include the diagonals that have length 1, specifically the ones at (0, height - 1) and (width - 1, 0). We are implementing an iterator that should not care about the way it's being used. Therefore, we don't care about the fact they don't need to be sorted.

Cool, let's leave the iterator itself to someone else, right?⁴

Implementing the iterator over diagonals

We can start with a simple skeleton based on the information that we pass from the diagonals. Also to utilize the matrix_t and also contain implementation details hidden away, we will put this code into the diagonals class.

class diagonals_iter {
    matrix_t& m;
    std::size_t x;
    std::size_t y;

public:
    diagonals_iter(matrix_t& matrix, std::size_t x, std::size_t y)
        : m(matrix)
        , x(x)
        , y(y)
    {
    }
};

In this case we will be implementing a “simple” forward iterator, so we don't need to implement a lot. Notably it will be:

• inequality operator (we need to know when we reach the end and have nothing to iterate over)
• preincrementation operator (we need to be able to move around the iterable)
• dereference operator (we need to be able to retrieve the objects we iterate over)

class diagonals_iter {
    matrix_t& m;
    std::size_t x;
    std::size_t y;

public:
    diagonals_iter(matrix_t& matrix, std::size_t x, std::size_t y)
        : m(matrix)
        , x(x)
        , y(y)
    {
    }

    bool operator!=(const diagonals_iter& rhs) const
    {
        // iterators are not equal if they reference different matrices, or
        // their positions differ
        return m != rhs.m || x != rhs.x || y != rhs.y;
    }

    diagonals_iter& operator++()
    {
        if (y != 0) {
            // iterating through diagonals down the first column
            y++;
            return *this;
        }

        // iterating the diagonals along the first row
        x++;
        if (x == m.front().size()) {
            // switching to diagonals in the first column
            x = 0;
            y++;
        }

        return *this;
    }

    diagonal<T> operator*() const { return diagonal { m, x, y }; }
};

Let's go one-by-one. Inequality operator is rather simple, just compare iterator's attributes field-by-field. If you think about it, checking inequality of two 2D vectors may be a bit inefficient, therefore, we can swap around and check it as a last thing.

-        return m != rhs.m || x != rhs.x || y != rhs.y;
+        return x != rhs.x || y != rhs.y || m != rhs.m;

Preincrementation is where the magic happens. If you have a better look, you can see two branches of this operation:

1. When y != 0 (we're iterating over the diagonals in the first column) In this case, we just bump the row and we're done.
2. When y == 0 (we're iterating over the diagonals in the first row) In this case, we bump the column and check if we haven't gotten out of bounds, i.e. the end of the first row. If we get out of the bounds, we're continuing with the second diagonal in the first column.

Dereferencing the iterator must “yield” something. In our case it will be the diagonal that we want to sort. For sorting we need just the iterators that can move around said diagonal. The simplest thing, we can do, is to delegate it to something else. In our case it will be a class called diagonal.

Implementing the diagonal itself

After implementing the iterator over diagonals, we know that all we need to describe a diagonal is the matrix itself and the “start” of the diagonal (row and column). And we also know that the diagonal must provide some iterators for the std::sort function. We can start with the following skeleton:

template <typename T>
class diagonal {
    using matrix_t = std::vector<std::vector<T>>;

    matrix_t& matrix;
    std::size_t x;
    std::size_t y;

public:
    diagonal(matrix_t& matrix, std::size_t x, std::size_t y)
        : matrix(matrix)
        , x(x)
        , y(y)
    {
    }

    diagonal_iter begin() const { return diagonal_iter { matrix, x, y }; }

    diagonal_iter end() const
    {
        auto max_x = matrix[y].size();
        auto max_y = matrix.size();

        // we need to find the distance in which we get out of bounds (either in
        // column or row)
        auto steps = std::min(max_x - x, max_y - y);

        return diagonal_iter { matrix, x + steps, y + steps };
    }
};

Initialization is rather simple, we just “keep” the stuff we get, begin is the simplest, we just delegate.

In case of the end, it gets more complicated. We need to know where is the “end” of the diagonal. Since end should point to the first element “after” the iterable, we know that it's the first position of the iterator where either y becomes matrix.size() or x becomes matrix[y].size(). Also we are moving along diagonal, duh, therefore we can deduce the first “position” afterwards by minimal amount of steps to get out of the any column or row, hence std::min(max_x - x, max_y - y). Final position is then computed simply by adding the steps to the beginning of the diagonal.

Now we just need to finish the iterator for the diagonal itself and we're done.

Implementing diagonal_iter

This part is the hardest from all we need to do. It's because of the requirements of the std::sort that requires us to implement a random access iterator. I have briefly described it above, and “in a nutshell” it means that we need to implement an iterator that can move in constant time along the diagonal in any amount of steps.

Let's go through all of the functionality that our iterator needs to support to be used in std::sort. We need the usual operations like:

• equality/inequality
• incrementation
• dereferencing

We will also add all the types that our iterator uses with the category of the iterator, i.e. what interface it supports:

class diagonal_iter {
    // we need to keep reference to the matrix itself
    matrix_t& m;

    // we need to be able to tell our current position
    std::size_t x;
    std::size_t y;

public:
    using difference_type = std::ptrdiff_t;
    using value_type = T;
    using pointer = T*;
    using reference = T&;
    using iterator_category = std::random_access_iterator_tag;

    diagonal_iter(matrix_t& matrix,
        std::size_t x,
        std::size_t y)
        : m(matrix)
        , x(x)
        , y(y)
    {
    }

    bool operator==(const diagonal_iter& rhs) const
    {
        return x == rhs.x && y == rhs.y && m == rhs.m;
    }

    diagonal_iter& operator++()
    {
        // we are moving along the diagonal, so we increment both ‹x› and ‹y› at
        // the same time
        x++;
        y++;
        return *this;
    }

    reference operator*() const { return m[y][x]; }
};

This is pretty similar to the previous iterator, but now we need to implement the remaining requirements of the random access iterator. Let's see what those are:

• decrementation - cause we need to be able to move backwards too, since _random _ access iterator extends the interface of bidirectional iterator
• moving the iterator in either direction by steps given as an integer
• being able to tell the distance between two iterators
• define an ordering on the iterators

Let's fill them in:

class diagonal_iter {
    // we need to keep reference to the matrix itself
    matrix_t& m;

    // we need to be able to tell our current position
    std::size_t x;
    std::size_t y;

public:
    using difference_type = std::ptrdiff_t;
    using value_type = T;
    using pointer = T*;
    using reference = T&;
    using iterator_category = std::random_access_iterator_tag;

    diagonal_iter(matrix_t& matrix,
        std::size_t x,
        std::size_t y)
        : m(matrix)
        , x(x)
        , y(y)
    {
    }

    bool operator==(const diagonal_iter& rhs) const
    {
        return x == rhs.x && y == rhs.y && m == rhs.m;
    }

    diagonal_iter& operator++()
    {
        // we are moving along the diagonal, so we increment both ‹x› and ‹y› at
        // the same time
        x++;
        y++;
        return *this;
    }

    reference operator*() const { return m[y][x]; }

    // exactly opposite to the incrementation
    diagonal_iter operator--()
    {
        x--;
        y--;
        return *this;
    }

    // moving ‹n› steps back is same as calling decrementation ‹n›-times, so we
    // can just return a new iterator and subtract ‹n› from both coordinates in
    // the matrix
    diagonal_iter operator-(difference_type n) const
    {
        return diagonal_iter { m, x - n, y - n };
    }

    // here we assume that we are given two iterators on the same diagonal
    difference_type operator-(const diagonal_iter& rhs) const
    {
        assert(m == rhs.m);
        return x - rhs.x;
    }

    // counterpart of moving ‹n› steps backwards
    diagonal_iter operator+(difference_type n) const
    {
        return diagonal_iter { m, x + n, y + n };
    }

    // we compare the coordinates, and also assume that those 2 iterators are
    // lying on the same diagonal
    bool operator<(const diagonal_iter& rhs) const
    {
        assert(m == rhs.m);
        return x < rhs.x && y < rhs.y;
    }
};

At this point we could probably try and compile it, right? If we do so, we will get yelled at by a compiler for the following reasons:

/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1792:11: error: object of type 'diagonal<int>::diagonal_iter' cannot be assigned because its copy assignment operator is implicitly deleted [clang-diagnostic-error]
          __last = __next;
                 ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1817:11: note: in instantiation of function template specialization 'std::__unguarded_linear_insert<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Val_less_iter>' requested here
            std::__unguarded_linear_insert(__i,
                 ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1849:9: note: in instantiation of function template specialization 'std::__insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
          std::__insertion_sort(__first, __first + int(_S_threshold), __comp);
               ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1940:9: note: in instantiation of function template specialization 'std::__final_insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
          std::__final_insertion_sort(__first, __last, __comp);
               ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:4820:12: note: in instantiation of function template specialization 'std::__sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
      std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
           ^
matrix-sort.cpp:161:18: note: in instantiation of function template specialization 'std::sort<diagonal<int>::diagonal_iter>' requested here
            std::sort(d.begin(), d.end());
                 ^
matrix-sort.cpp:17:19: note: copy assignment operator of 'diagonal_iter' is implicitly deleted because field 'm' is of reference type 'diagonal<int>::matrix_t &' (aka 'vector<std::vector<int>> &')
        matrix_t& m;
                  ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1830:2: error: no matching function for call to '__unguarded_linear_insert' [clang-diagnostic-error]
        std::__unguarded_linear_insert(__i,
        ^~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1850:9: note: in instantiation of function template specialization 'std::__unguarded_insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
          std::__unguarded_insertion_sort(__first + int(_S_threshold), __last,
               ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1940:9: note: in instantiation of function template specialization 'std::__final_insertion_sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
          std::__final_insertion_sort(__first, __last, __comp);
               ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:4820:12: note: in instantiation of function template specialization 'std::__sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
      std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
           ^
matrix-sort.cpp:161:18: note: in instantiation of function template specialization 'std::sort<diagonal<int>::diagonal_iter>' requested here
            std::sort(d.begin(), d.end());
                 ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1782:5: note: candidate template ignored: substitution failure [with _RandomAccessIterator = diagonal<int>::diagonal_iter, _Compare = __gnu_cxx::__ops::_Val_less_iter]
    __unguarded_linear_insert(_RandomAccessIterator __last,
    ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1923:11: error: object of type 'diagonal<int>::diagonal_iter' cannot be assigned because its copy assignment operator is implicitly deleted [clang-diagnostic-error]
          __last = __cut;
                 ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1937:9: note: in instantiation of function template specialization 'std::__introsort_loop<diagonal<int>::diagonal_iter, long, __gnu_cxx::__ops::_Iter_less_iter>' requested here
          std::__introsort_loop(__first, __last,
               ^
/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:4820:12: note: in instantiation of function template specialization 'std::__sort<diagonal<int>::diagonal_iter, __gnu_cxx::__ops::_Iter_less_iter>' requested here
      std::__sort(__first, __last, __gnu_cxx::__ops::__iter_less_iter());
           ^
matrix-sort.cpp:161:18: note: in instantiation of function template specialization 'std::sort<diagonal<int>::diagonal_iter>' requested here
            std::sort(d.begin(), d.end());
                 ^
matrix-sort.cpp:17:19: note: copy assignment operator of 'diagonal_iter' is implicitly deleted because field 'm' is of reference type 'diagonal<int>::matrix_t &' (aka 'vector<std::vector<int>> &')
        matrix_t& m;
                  ^

That's a lot of noise, isn't it? Let's focus on the important parts:

/usr/bin/../lib/gcc/x86_64-redhat-linux/12/../../../../include/c++/12/bits/stl_algo.h:1792:11: error: object of type 'diagonal<int>::diagonal_iter' cannot be assigned because its copy assignment operator is implicitly deleted [clang-diagnostic-error]
…
matrix-sort.cpp:17:19: note: copy assignment operator of 'diagonal_iter' is implicitly deleted because field 'm' is of reference type 'diagonal<int>::matrix_t &' (aka 'vector<std::vector<int>> &')
        matrix_t& m;
                  ^

Ah! We have a reference in our iterator, and this prevents us from having a copy assignment operator (that is used “somewhere” in the sorting algorithm). Well… Let's just wrap it!

# we need to keep a different type than reference
-        matrix_t& m;
+        std::reference_wrapper<matrix_t> m;

# in comparison we need to get the reference out of the wrapper first
-            return x == rhs.x && y == rhs.y && m == rhs.m;
+            return x == rhs.x && y == rhs.y && m.get() == rhs.m.get();

# same when we return a reference to the “cell” in the matrix
-        reference operator*() const { return m[y][x]; }
+        reference operator*() const { return m.get()[y][x]; }

# and finally in the assertions that we set for the “distance” and “less than”
-            assert(m == rhs.m);
+            assert(m.get() == rhs.m.get());

We're done now! We have written an iterator over diagonals for a 2D vector. You can have a look at the final result here.

Footnotes

1. just because I'm used to it and don't care about your opinion ;) ↩

2. exercise at your own risk ↩

3. me in 5 minutes in fact, but don't make me scared ↩

4. me in the next section… ↩